Fraktale - Unregelmäßig geformte Dinge in der Natur
In der Natur sind viele Dinge unregelmäßig geformt. Mit Hilfe der klassischen Geometrie lassen sich Objekte, wie z.B. ein Würfel, eine Kugel, ein Zylinder oder eine Pyramide exakt beschreiben. Mit Hilfe der fraktalen Geometrie lassen sich die unregelmäßig geformten Strukturen in der Natur beschreiben. Das Wort "fraktal" stammt von dem lateinischen "Fraktus", was soviel bedeutet wie gebrochen, zerklüftet, unregelmäßig.
Fraktale sind unregelmäßige Objekte, die keinen glatten Rand haben und sich nicht in einfache geometrische Elemente zerlegen lassen. Eine weitere Eigenschaft von Fraktalen ist ihre Selbstähnlichkeit. Die Struktur von verschieden großen Ausschnitten bleibt ähnlich.
Ideale geometrische Fraktale lassen sich durch relativ einfache mathematische Rechenvorgänge herstellen, wie z. B. bei der so genannten "Koch-Kurve".
Die Koch-Kurve oder kochsche Kurve wurde im Jahre 1904 von dem schwedischen Mathematiker Helge von Koch beschrieben.
Bei der Koch-Kurve wird eine Strecke in drei gleichgroße Abschnitte aufgeteilt:

Dann wird der mittlere Abschnitt entfernt und durch ein Dreieck ersetzt:

Als nächstes wird jedes der vier Teilstücke wieder in drei gleichgroße Abschnitte aufgeteilt:

Der jeweils mittlere Abschnitt wird wieder entfernt und durch ein Dreieck ersetzt:

Dieser Vorgang wird fortgesetzt: (Man bezeichnet diesen Vorgang auch als "Iteration".)



Das Wort "Iteration" stammt von dem lateinischen "iterare", was soviel bedeutet wie "wiederholen".
Je weiter die Iteration fortgesetzt wird, also je mehr Dreiecke in der Mitte jeder Linie eingefügt werden, desto runder und glatter wird der Rand der Kurve.
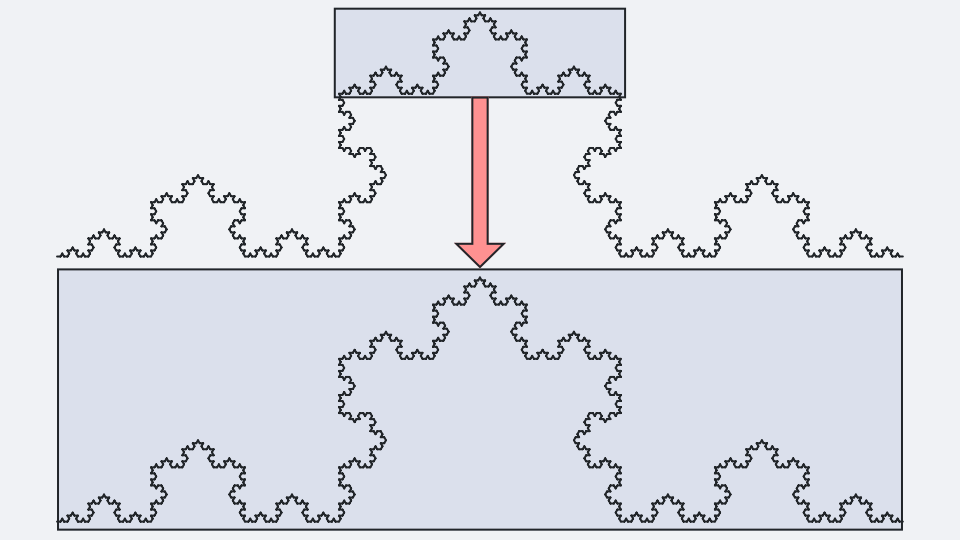
Erst wenn die Anzahl der Iterationen unbegrenzt ist, handelt es sich um die Koch-Kurve. Bei der Koch-Kurve geht die Selbstähnlichkeit bis in die Unendlichkeit...

...Das hat zur Folge, dass ein kleiner Ausschnitt der Koch-Kurve, der dann wieder vergrößert wird, genauso aussieht, wie die ursprüngliche Koch-Kurve.
Bei der Koch-Kurve handelt es sich um eine exakte oder strikte Selbstähnlichkeit.
Real existierende Beispiele aus der Natur sind selbstähnlich, nicht jedoch strikt selbstähnlich!
Ein Baum ist ein fraktales Objekt, der mit seinen Ästen eine ähnliche Struktur wie der Ast mit seinen kleineren Ästen und Zweigen hat.

Es gibt jedoch keine zwei Äste, die exakt gleich aussehen. Die Eigenschaft der Selbstähnlichkeit ist also vorhanden, jedoch keine strikte Selbstähnlichkeit, wie bei der Koch-Kurve.
Beim Baum zeigen sich auch nur einige wenige Iterationen. An einem großen Ast befinden sich kleinere Äste und Zweige, dann kommen aber schon die Blätter und die Selbstähnlichkeit stößt an ihre natürliche Grenze.
In der Natur gibt es noch viele weitere Beispiele für Objekte mit fraktalen Eigenschaften, wie z.B. bei einer Küstenlinie.
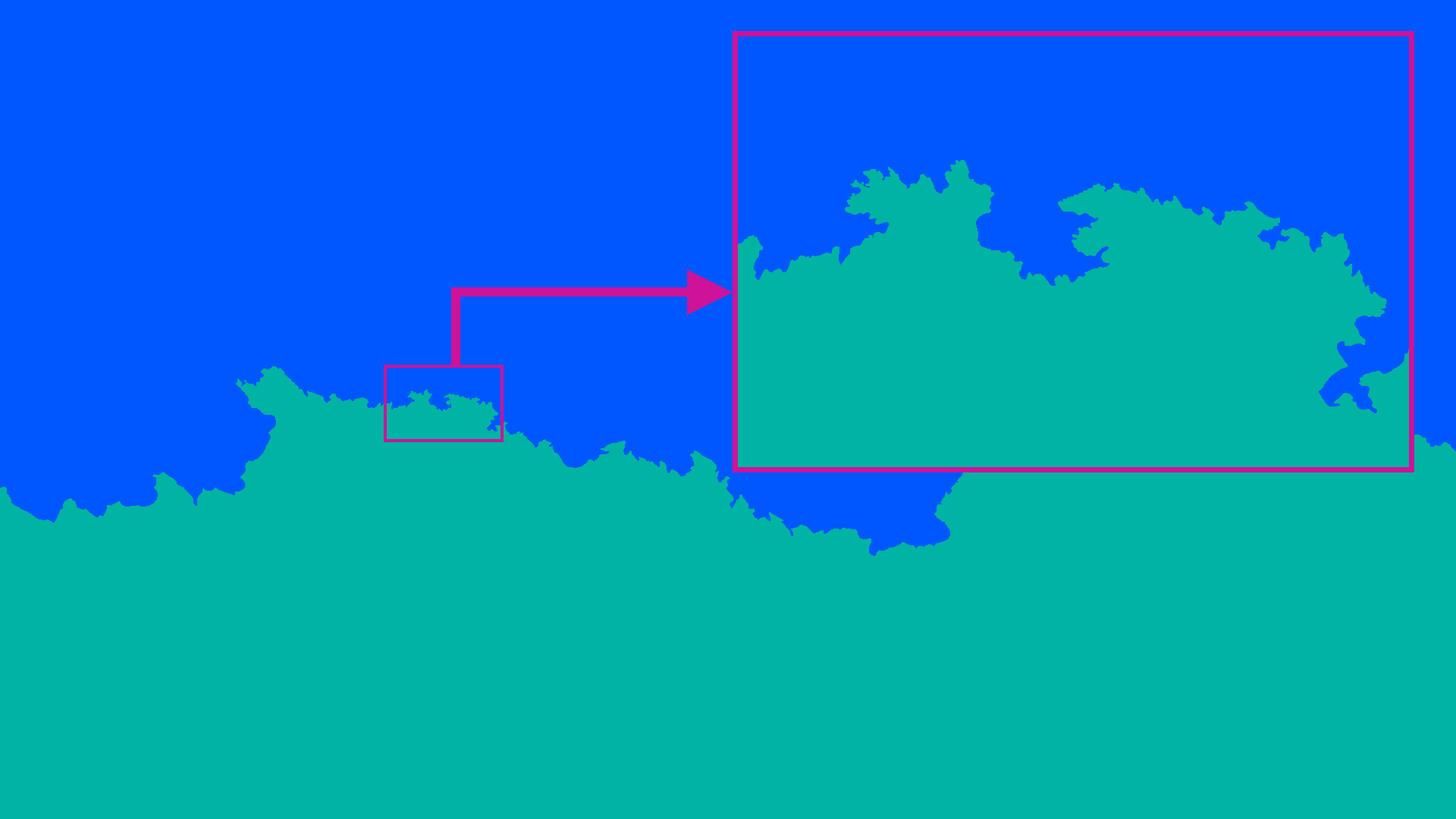
Ein kleiner Ausschnitt der Küstenlinie hat eine ähnlich zerklüftete Struktur, wie die gesamte Küstenlinie...
...Aus dem Vergrößerungsausschnitt kann erneut ein kleiner Ausschnitt heraus genommen und vergrößert werden. Die Ähnlichkeit bleibt erhalten.
Ebenso wie der Rand einer zerklüfteten Küstenlinie, lässt sich auch der Rand einer Wolke oder z.B. einer Galaxie vergrößern, wobei die Ähnlichkeit der ursprünglichen Struktur erhalten bleibt.

Wie beim Baum, können auch hier die Iterationen nicht unbegrenzt fortgesetzt werden.
Die Selbstähnlichkeit stößt an ihre natürliche Grenze, im Gegensatz zur Koch-Kurve, bei der es sich um eine mathematische Konstruktion handelt und nicht um ein natürliches Objekt, wie beispielsweise ein Baum, eine Wolke, eine Küstenlinie oder eine Galaxie.
